& Continuous Learning

RAID 5 is a pretty magical thing overall, though a large portion of its magic lies in how it works on a bitwise level. But before I get into the bitwise sorcery, I'd like to briefly explain what RAID5 is. RAID stands for Redundant Array of Inexpensive (or Independent) Disks. There are a number of different types of RAID such as RAID0, RAID1, RAID5 and RAID6 which each store data in different ways and have different space efficiencies and fault tolerances.

Space efficiency is given as amount of storage space available in an array of n disks, in multiples of the capacity of a single drive. For example if an array holds n=5 drives of 250GB and efficiency is n-1 then available space is 4 times 250GB or roughly 1TB.

The space efficiency of RAID5 is n-1 and the fault tolerance allows for one disk to go down at a time. What this means is that if you have a RAID5 array set up, you lose one of your disk's worth of space in the array, yet if any one of the disks in the array goes down, you do not lose any data. Compared to something like RAID1 which simply mirrors all data so that what is stored on one disk is also stored on another, RAID5 has a much better space efficiency.

Now if you're like me, you probably wondered, "How the hell is RAID5 possible? Where do they fit the data? If you back up data, shouldn't it all be duplicated somewhere? How is it possible to have space efficiency less than 1/2 n? Isn't there some conservation of mass law that prevents such a preposterously awesome thing from happening?" To understand the answer to the question, we have to look at the bitwise level of RAID5, or how the data is really stored in 1's and 0's. And this, my friend, is where the mysterious and beautiful Exclusive Or (XOR) operator comes in.

Many of you are familiar with AND and OR operators, AND only evaluates to true when both inputs are true, while OR only evaluates to false when both inputs are false. The mathematical miscreant we know as "XOR" only evaluates to true when both of its inputs are opposite. So, to quickly summarize the XOR function, take a look at the following truth table:

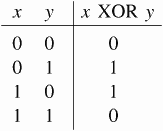
Got it? Good.

XOR has a few other interesting properties as well, the most important of which is that it is reversible. That is, if you XOR A and B to get result C, then you can get A back by doing B XOR C, or get B back by doing A XOR C. This can be extended so that if you do (A XOR B) XOR C = D, then you can do the same thing to get back any of the data stored in A, B, or C, by applying the exclusive or operator to D and the other two inputs. Don't believe me? Let's do an example:

Let's say A = 0010, B = 0101, and C = 1100. So D would be equal to the XOR of all three:

 (A XOR B XOR C)
= (0010 XOR 0101) XOR C
= 0111 XOR C
= 0111 XOR 1100
= 1011
= D

So now if for some reason we lost one of the inputs, (A, B, or C), we can use D and two of the other inputs to get that one back.  So let's say we lose B, we can get the data it contained back by XOR-ing the other three parts together:

A XOR C XOR D
= 0010 XOR 1100 XOR D
= 1110 XOR 1011
= 0101
= B

Did I just blow your mind? Some people call it "math." Others call it "logic." I call it like I see it and that XOR is straight up witchcraft.

Well all fantasy aside, the above example has some very practical applications for data storage. RAID5 uses this unique property of XOR to sort of stack data on top of each other into a storage unit called the "parity block" or "parity drive" (datum D in the example above would be considered the parity datum.) But the concept of RAID5 is a little more complicated than just abstracting the A, B, C, and D example from above to apply to whole drives instead of just 4-bit numbers. RAID5 uses something called "striping" to store data. Each drive in a RAID5 array is "striped" into parts so that when you store data, you store it across all the drives in the array. The concept of "striping" is probably best described the aid of the following picture:

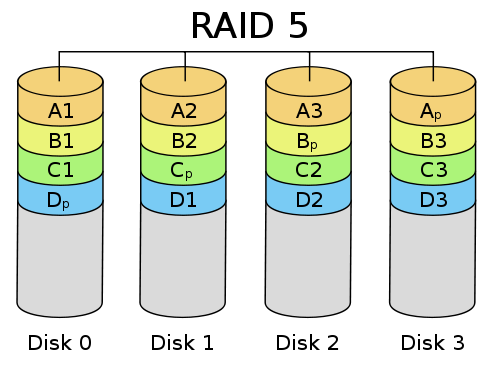
Each of the four drives in the picture above is divided into four blocks, each belonging to a stripe on the same level across each drive. Each drive and each stripe have a parity block which is the XOR of the other three blocks. In the picture this is denoted by the subscript "p." The fault tolerance for this set up with striping works just like the example above but repeated for every stripe. So say you lost drive 3, you would XOR A₁ with A₂ and A_p to get the remaining A₃ for the A stripe, B₁ with B₂ and B₃ to get your parity block, and then the same with C and D to get those bits of data back.

And that, in short, is how RAID5 works.

Sources:

RAID wiki

How RAID5 works